From Paint to PhotoShop real quick: Generating photo-realistic images using semantic image synthesis

Have you heard the latest buzz from NVDIA? Their engineers where able to create an algorithm that converts semantic images, the ones that you doodle in MS Paint as a toddler, to very realistic images.

Just look at this animation:

I was not born with artistically coordinated hands. I can’t even draw passable stick figures. My right hand sketches are practically as bad as my left. Having a physics background only worsened this ‘skill’ as I was trained to assume and over simplify 3D moving objects as 1D dots and particles connected with hasty crooked arrows. I find art fun but I guess it’s not mutual.

Now, with the advent of deep learning and machine learning in image processing, we can all be the Van Goghs and Picassos that we dreamed of.

To start, here is a link of their paper if you don’t want any spoilers.

This paper is state-of-the-art in image segmentation and style transfer as of writing so brace yourselves with some maths and ramp up your machine-learning curves.

Image Processing Basics

There are two main things that you can do with image processing: classification and generation. Image classification involves various algorithms that categorizes an existing image into a particular class.

Like this Meme:

Visually an image classifier algorithm looks like this:

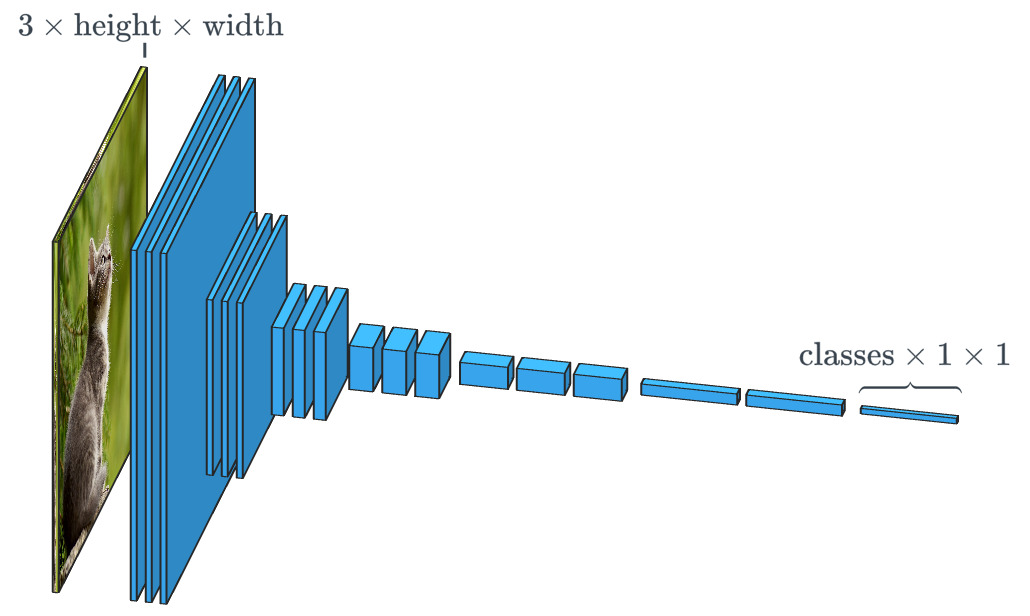
Basically, you have an image with 3 channels (red, green and blue) and height-width dimension. You apply image decomposition techniques and output a value that you use to classify an image (cat or dog based from the meme above).

On the other hand, image generation is when you create new images from certain inputs. This time around you make use of that little information to reconstruct an image or generate an entirely new image.

The main imaging technique to achieve both these processes is called convoltion. In simplest terms, convolution is just multiplication in frequency space. Read my post on Fourier Transforms, Convolution, and Image Formation.

Another term for image classifiers are discriminators. A convolution operation reduces the dimension of features based from a pixel window:

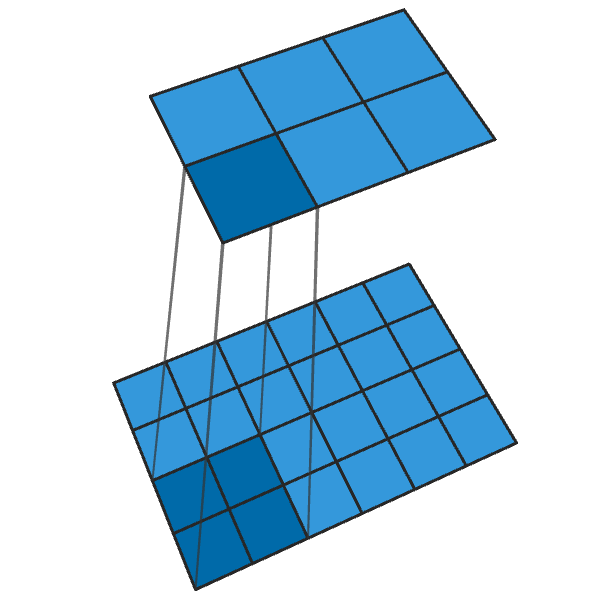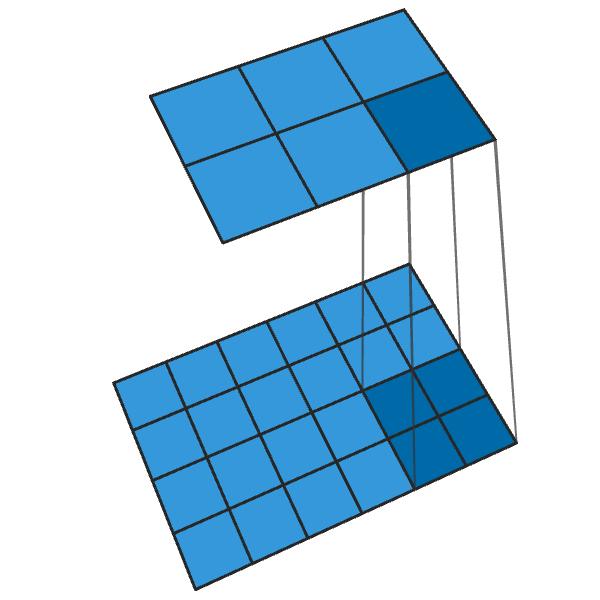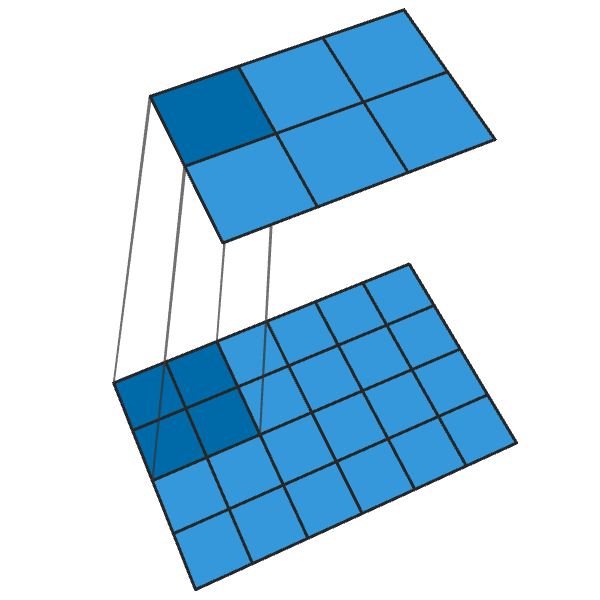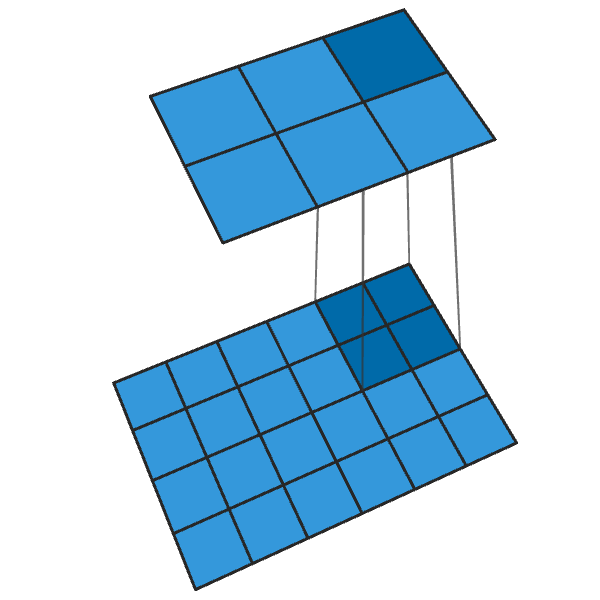
Image generation works with the same principle but done in reverse.

As a baseline to measure the performance, an image classifier can be cross-validated with a ground truth. The problem is the baseline for testing the performance of an image generator. This problem is addressed by a type of network algorithm called Generative Adversarial Network (GAN).

Adversarial because you will train to models that will compete with each other. The generator produces fake images that will be fed as one of the inputs to the discriminator. The discriminator will then try to identify whether the input image is real or fake.

To train the models and make it adaptively learn, we use a loss function given by:

\[\begin{equation} \mathcal{L}_\text{GAN}(D, G) = \underbrace{E_{\vec{x} \sim p_\text{data}}[\log D(\vec{x})]}_{\text{accuracy on real images}} + \underbrace{E_{\vec{z} \sim \mathcal{N}}[\log (1 - D(G(\vec{z}))]}_{\text{accuracy on fakes}} \end{equation}\]

Consider \(x\) is the input image. If the discriminator \(D\) is accurate in identifying real images, then first term on the right hand side of the equation should be low. If \(D\) correctly identifies fake images, the expectation value of the last term should also be low.

The goal is to diminish the value of the loss function to increase the competence of the models.

GANs are amazing in its job for this type of image processing. However, they are sensitive to noise thus are very hard to train. For example if \(D\) is almost always misclassifying the fake images as real, then the model has the tendency to produce a single image that is lossy and unrealistic. Experts call this the collapse.

To solve this dilemma, previous studies have focused on modifying the loss function and and gradually increasing the image resolution each training step.

GANs can also be expanded to image-to-image translation. That is instead of a random input vector for the generator, the input can be an image, say for example a semantic image and generate a synthetic image. The discriminator on the other hand compares the semantic image and the original image and decide whether its real or not.

The problem with the current GAN setup is that the convolution operation across the training steps and layers combine only patches that are small relative to the usual training images making too slow and unreliable still.

One not-to-old method to solve this is the pix2pixHD algorithm. It utilizes skip connections by training portions of the network with lower resolution images, appending it other layers and trained again on higher resolution images.

Going back to the previous GANs, most of them uses batch normalization to boost speed and training stability. This is done with a batch of images through this equation:

\[y = \frac{x - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

Essentially, the mean of the features are translated to 0 and the standard deviation to 1. However, this method is still gruesome because each layer of the network should be adapting to the new parameter values.

The pix2pixHD resolves this by implementing instance normalization which normalizes over each image separately reducing training time.

pix2pixHD performs well except when it doesn’t. Case in point if there is only a single class in the semantic image. Since it is doing an instance normalization with identical values for each channel, convolution operation will flatten out the features ultimately throwing away information from the semantic image.

This is where SPADES comes in. SPADES stands up for spatially-adaptive [de]normalization. It augments the pix2pix framework by preventing the loss semantic information. This is done by using downsampled versions of the semantic image to modulate the normalized outputs of each training layer.

Now can revert back to the original GAN implementation with only the random vector as input. Since the semantic image is integrated to the network itself, we have the ability to input as many image as we can.

Lastly, if we have a another input image that we can train, pass through an encoder, and spit out generator vectors, the SPADE will also reproduce an image copying the style of the encoded input image.

Here are some results:

Just imagine the possibilities that we can do with this synthetic image generation. Maybe we can even create our own high-definition movies from rough sketches come the future.

Want to collaborate? Message me in LinkedIn.

References:

[1] T. Park, etal. Semantic Image Synthesis with Spatially Adaptive Normalization.

[2] A. King. Photos from Crude Sketches: NVIDIA’s GauGAN Explained Visually.